The Tabulator

While simulation via direct propagation can be vastly more efficient and precise than looking up average photoelectron yields from tables, it is impractical to use the same technique in reconstruction, where the locations of the light sources are not exactly known. Instead, it is significantly more efficient to compare the observed photoelectron counts to a table of precomputed average photoelectron yields for all possible source-receiver orientations.

In the past such tables were made with Photonics and then parameterized with 6-dimensional tensor-product B-spline surfaces using Photospline. Photonics provided a good description of the optical properties of the ice as they were known at the time, but newly discovered features of photon transport in the ice, such as the azimuthal anisotropy of scattering, are fundamentally incompatible with its basic assumptions. In order to be able to tabulate photon detection probabilities including these effects, we have added a tabulation mode to clsim that is similar to Photonics, but shares the propagation code used in clsim’s well-tested direct propagation mode. This mode is also moderately faster than Photonics (\(\sim 15\%\) on typical systems).

Quickstart

The main user interface is the following tray segment. The script resources/tablemaker/photomc.py demonstrates its usage.

icecube.clsim.tablemaker.TabulatePhotonsFromSource(tray, name, PhotonSource='cascade', Zenith=0.0, Azimuth=0.0, ZCoordinate=0.0, Energy=1.0, FlasherWidth=127, FlasherBrightness=127, Seed=12345, NEvents=100, IceModel='spice_mie', DisableTilt=False, Filename='', TabulateImpactAngle=False, PhotonPrescale=1, Axes=None, Directions=None, Sensor='DOM', RecordErrors=False, UseGeant4=False, HoleIce='as.h2-50cm')

Tabulate the distribution of photoelectron yields on IceCube DOMs from various light sources. The light profiles of the sources are computed from the same parameterizations used in PPC, but like in the direct propagation mode can be computed using GEANT4 instead.

The mode of tabulation is controlled primarily by the PhotonSource parameter.

  • ‘cascade’ will simulate an electromagnetic cascade of Energy GeV at (0, 0, ZCoordinate), oriented according to Zenith and Azimuth. The default coordinate system is spherical and centered the given vertex, with 200 quadratically spaced bins in radius, 36 linear bins in azimuthal angle (only from 0 to 180 degrees by default), 100 linear bins in the cosine of the polar angle, and 105 quadratic bins in time residual w.r.t the direct path from (0, 0, ZCoordinate).

  • ‘flasher’ will simulate a 405 nm LED flasher pulse with the given FlasherWidth and FlasherBrightness settings. The source position and coordinate system are the same as for the ‘cascade’ case.

  • ‘infinite-muon’ will simulate a “bare” muon of infinite length. The coordinate system is cylindrical and centered on the axis of the muon. Since the muon’s position is degenerate with time, the usual parallel distance is replaced by the z coordinate of the closest approach to the detection position, and the starting positions of the simulated muons are sampled randomly (ZCoordinate is ignored). There are 100 quadratic bins in perpendicular distance to the source axis, 36 linear bins in azimuthal angle (0 to \(\pi\) radians), 100 linear bins in z coordinate of closest approach, and 105 quadratic bins in time residual w.r.t. the earliest possible Cherenkov photon.

Parameters:

  • PhotonSource – the type of photon source (‘cascade’, ‘flasher’, or ‘infinite-muon’).

  • Zenith – the orientation of the source

  • ZCoordinate – the depth of the source

  • Energy – the energy of the source (only for cascade tables)

  • FlasherWidth – the width of the flasher pulse (only for flasher tables)

  • FlasherBrightness – the brightness of the flasher pulse (only for flasher tables)

  • Seed – the seed for the random number service

  • NEvents – the number of events to simulate

  • RecordErrors – record the squares of weights as well (useful for error bars)

  • IceModel – the path to an ice model in $I3_BUILD/ice-models/resources/models/ICEMODEL. Likely values include: ‘spice_mie’ ppc-style SPICE-Mie parametrization

  • DisableTilt – if true, disable tilt in ice model

  • Filename – the name of the FITS file to write

  • TabulateImpactAngle – if True, tabulate the impact position of the photon on the DOM instead of weighting by the DOM’s angular acceptance

  • Axes – a subclass of clsim::tabulator::Axes that defines the coordinate system. If None, an appropriate default will be chosen based on PhotonSource.

  • Directions – a set of directions to allow table generation for multiple sources. If None, only one direction given by Zenith and Azimuth is used.

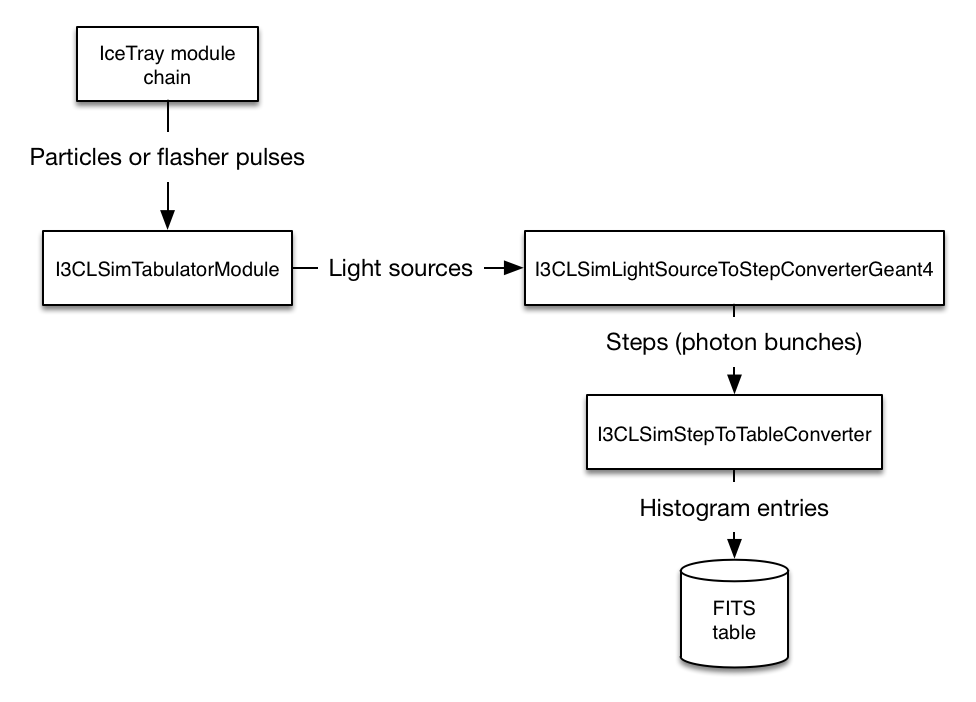
Architecture

The data flow in the tabulation mode is very similar to the direct tracking mode, except that I3CLSimModule is replaced with I3CLSimTabulatorModule, which in turn passes photon bunches to I3CLSimStepToTableConverter instead of I3CLSimStepToPhotonConverterOpenCL, as illustrated in the flow chart below. Both of these replacement classes are significantly similar to their direct-propagation counterparts.

../../_images/tabulator_flow.png

Common components

As in direct propagation, a few components are needed to describe how photons are generated, propagated, and detected.

  • The parameterization list describes the photon emission profiles of various kinds of light sources.

  • The spectrum table is optional, and describes the emission spectra of any non-Cherenkov light sources that will be simulated (e.g. LED flashers).

  • The wavelength acceptance of the DOM describes the quantum efficiency (QE) of the receiver, and is used to compute the effective spectrum of detected Cherenkov photons. This bears some explanation. In Photonics simulation, photons were drawn directly from a Cherenkov spectrum (\(\propto \lambda^{-2}\)) between 300 and 600 nm and then weighted by the QE of the receiver when a bin entry was recorded. In our tabulation we instead draw photon wavelengths from the QE-weighted Cherenkov spectrum, and skip the later QE weighting step, reducing the variance in the final histogram. This means that each of our photons represents on average more than one photon in the Photonics sampling scheme. The “number of photons” recorded for normalization purposes includes a scale factor to account for this.

  • The angular acceptance of the DOM describes the relative sensitivity of the receiver as a function of the photon impact angle, and is used to compute the photon detection probability each time a photon position is recorded.

  • The medium properties describe the scattering and absorption characteristics of the medium through which photons are being tracked.

Components unique to tabulation

class clsim::tabulator::Axis

Describes how to map a double-precision coordinate to a bin index. The bins are linearly spaced under some transformation supplied by the concrete instance of Axis.

Axis(double min, double max, unsigned n_bins)
Parameters:

  • min – the left-hand edge of the first bin (in coordinate space)

  • max – the right-hand edge of the last bin (in coordinate space)

  • n_bins – the number of bins. There will be n_bins+1 bin edges.

double Transform(double value) const

Apply transformation from linear to nonlinear space

std::string GetTransformCode(const std::string &varName) const

Generate OpenCL code that transforms a value from linear to nonlinear space

double InverseTransform(double value) const

Apply transformation from nonlinear to linear space

std::string GetInverseTransformCode(const std::string &varName) const

Generate OpenCL code that transforms a value from nonlinear to linear space

Currently there are only two concrete implementations of Axis:

class clsim::tabulator::LinearAxis

An axis with a trivial linear scale

class clsim::tabulator::PowerAxis

An axis with bins spaced according to a power

PowerAxis(double min, double max, unsigned n_bins, unsigned power = 1)
Parameters:

  • min – the left-hand edge of the first bin (in coordinate space)

  • max – the right-hand edge of the last bin (in coordinate space)

  • n_bins – the number of bins. There will be n_bins+1 bin edges.

  • power – the power of the transformation (e.g. 1 for linearly spaced bins, 2 for quadratically spaced bins, 3 for cubic, etc)

class clsim::tabulator::Axes

A description of the coordinate system of the photon detection probability table

Axes(const std::vector<boost::shared_ptr<clsim::tabulator::Axis>> &axes)
std::string GetCoordinateFunction() const

Generate an OpenCL function that calculates the source-relative coordinates from the photon position and time

std::string GetBoundsCheckFunction() const

Generate an OpenCL function that returns true if the photon has exited the recording volume and should be stopped

double GetBinVolume(const std::vector<size_t> &multiIndex) const

Calculate the volume in cubic meters of a histogram bin.

Parameters:

multiIndex – a vector of bin indices in each dimension.

Currently there are two concrete implementations of Axes:

class clsim::tabulator::SphericalAxes

Spherical, source-centered coordinates, appropriate for approximately point-like emitters.

The dimensions are:

  • radius: distance (meters) from the position of the reference particle (i.e. length of the displacement vector)

  • azimuth: angle (degrees) of rotation of the displacement vector around the reference particle direction, measured w.r.t. a vector perpendicular to the reference particle pointed towards positive z (\(\vec{\rho}\) in Fig. 1 of the Photonics paper). The range from 180 to 360 degrees is mirrored onto 0 to 180 degrees.

  • polar angle: cosine of the opening angle between the reference particle direction and the displacement vector.

  • time residual: difference (in nanoseconds) between the photon detection time and the straight-line time from the reference particle position at \(c/n\). The reference time is calculated using the smallest group index of refraction in the wavelength range covered by the ice model to ensure that time residuals are always positive.

class clsim::tabulator::CylindricalAxes

Cylindrical coordinates centered on the axis of the source, appropriate for infinite-ranged particles moving at the speed of light (e.g. an approximation to high-energy muons).

The dimensions are:

  • perpendicular distance: distance of closest approach of the source to the receiver position (length of the \(\vec{\rho}\) vector in Fig. 1 of the Photonics paper).

  • azimuth angle (radians) of rotation rotation of the displacement vector around the reference particle direction.

  • z: IceCube z coordinate of position of closest approach of the source to the receiver position.

  • time residual difference (in nanoseconds) between the photon detection time and the earliest possible Cherenkov photon arrival time. This is given by the to move along the source direction at the speed of light and then to the receiver at the local speed of light at the Cherenkov angle. This time is calculated using the smallest index of refraction.

Open issues

  • All coordinate systems cover only half of the sphere/cylinder (like in Photonics). This is fine as long as the medium is symmetric under reflections across the plane containing \(\vec{\rho}\), which can only be true for all \(\vec{\rho}\) if the medium is symmetric around the z axis. To fully capture the azimuthal asymmetry, we have to record in the full volume and make tables for sources from all azimuths.

  • For cascades the center of the spherical coordinate system is the cascade vertex, not the shower maximum. While physically correct, this is different from the reference point in Photonics simulation, where the shower was compressed down to a point.

  • There are no over- or under-flow bins. For dimensions like azimuth or polar angle that cannot be out of range this is fine, but is a bit wrong for e.g. radius.

  • The DOM is currently treated as point-like, i.e. the point at which the photon is recorded is identical to center of the DOM. At source-receiver distances much larger than the DOM radius this is clearly negligible, but it might make a difference at very close range. It might be possible to fix by displacing the point at which the photon is recorded to the center of a sphere (or more properly, hemisphere) that intersects the current recording point.

  • There’s no way for the user to directly set the number of photons to be propagated. The step generators would need to gain some concept of a prescale to make this happen.